Ⅰ. 생산함수
1. 생산함수
• 일정기간 동안 생산요소의 투입량(Input)과 산출량(Output)과의 관계를 나타낸 함수
• 유량(Flow)의 개념으로서 일정 기간 동안의 산출량과 생산요소의 양과의 관계
- 유량은 일정 기간(1일, 1개월 등)에 대해서 측정하는 변수
- 저량(貯量)이란 일정 시점(2018년 12월 31일)에 대해서 측정하는 변수
: 예시 - 소득은 유량이고, 재산은 저량
• 생산함수는 생산요소의 수량이 주어져 있을 때 기술적으로 가장 효율적인 생산기술을 이용하여 생산할 수 있는 최대 산출량 수준을 보여줌
- 생산함수는 기술적으로 가장 효율적인 기술적 효율성(Technical efficiency)을 달성한 것을 나타냄
- 경제적 효율성(Economic efficiency) 개념이 전혀 개입되지 않았음
• 생산요소(Input, Factor of production)
- 노동(Labor)과 자본(Capital)
: 노동
> 인간 그 자체
: 자본
> 다른 재화를 생산하기 위하여 인간이 만들어 낸 생산요소(예: 기계, 공장, 토지 등)
• 가변생산요소(Variable input)
- 투입된 양이 변하는 생산요소
• 고정생산요소(Fixed input)
- 한 번 투입되면 양이 변하지 않는 생산요소
• 생산함수의 예

2. 단기 생산함수와 한계생산 체감
• 단기(Short-run)
- 고정생산요소가 존재하는 기간
• 장기(Long-run)
- 모든 생산요소가 가변생산요소인 기간
• 가변생산요소가 하나일 때(자본이 한 단위로 고정될 때)
- 생산함수 q = f(L, K) = f(L, 1) = g(L)
: 독립변수가 2개에서 하나로 변하므로 함수형태도 f에서 g로 변함
• 예시 <가래(Shovel)를 이용하여 터파기 공사를 하는 건설 회사>
- 가래(Shovel)를 이용하여 터파기 공사를 하는 건설회사를 상상할 때, 이 기업의 자본은 가래 1대이고, 근로자를 고용하여 터파기 공사를 함
- 가래란 흙을 파는 농기구의 하나로, 그림에서처럼 쇠 날을 끼운 가래의 넓죽한 몸에 자루를 박고,몸 양편 구멍에 줄을 매어 한 사람이 자루를 잡고 두 사람이 줄을 당기어 흙을 퍼 던지는 형태가일반적임
- 가래는 3명씩 한 조가 되어 작업하므로 2번째 근로자가 새로이 투입되는 경우 산출량의 증가(0.7) 보다 3번째 근로자가 새로이 투입되는 경우 산출량의 증가(0.8)보다 큼
- 4번째 근로자가 새로이 투입되는 경우 산출량의 증가는 0.7로서 감소하기 시작함
- 8번째 근로자가 새로이 투입되는 경우 산출량은 증가하지 않고, 그 이후에는 0 이하가 됨
- 근로자의 숫자가 4명을 초과하면 한계생산은 감소함
: 한계생산 체감의 법칙(Law of decreasing marginal product)
: 수확체감의 법칙(Law of diminishing returns)
• 노동투입량과 총생산량(m3 ), 한계생산량, 평균생산량

• 노동의 한계생산

• 총생산을 가로축에 노동, 세로축에 산출량(m3 )의 그래프

- 생산요소인 노동 투입량을 1단위 증가시킬 경우 증가되는 산출량
- 총생산곡선의 직사각형으로 표시
- 이 사각형을 다른 그래프로 표시하면 한계생산곡선이 됨
- 한계생산은 총생산곡선의 기울기와 같음

- 한계생산곡선 그래프의 직사각형을 합하면 총생산곡선이 됨
- 단위를 무한대로 나눌 수 있다면 그래프는 부드러운 곡선이 됨
• 노동의 평균생산

3. 장기 생산함수와 한계기술대체율의 체감
• 모든 생산요소가 가변생산요소이고 두 개인 경우(자본과 노동이 모두 가변생산요소인 경우)

• 생산함수는 3개의 변수(1개의 종속변수 q, 2개의 독립변수 K, L)가 개입되므로 3차원(q, K, L)의공간에 표시 가능
• 독립변수를 2차원 직각 좌표로 그리고, 종속변수를 직각좌표에 숫자로 표시할 수도 있는데,이것이 등량곡선(Ioquant)임
1) 등량곡선
• 동일한 수량의 산출량(숫자로 표시)을 생산할 수 있게 만드는 생산요소의 조합들로 구성된 집합
- 생산함수를 2차원 평면에 표시하는 등량곡선(Isoquant)으로 나타낼 수 있음
- 소비자 이론에서 효용함수를 무차별 곡선으로 나타낸 것과 동일한 원리
- 무차별곡선의 숫자는 서수적 의미이지만 등량곡선의 의미는 기수적 의미임

• 2가지 극단적인 경우의 등량곡선
- 등량곡선이 직선임
: 생산함수가 q = L + K
(노동과 자본이 대체관계에 있는 경우)
- 등량곡선이 L자형인 경우
: 생산함수가 min{K, L} : (Leontieff 생산함수)
• 일반적인 생산함수는 2가지 경우의 중간에 존재하고, 등량곡선은 다음과 같은 4가지 성질을 가짐
- 등량곡선은 우하향하는 모양을 가짐
- 원점에서 멀리 떨어진 등량곡선일수록 더 높은 생산량을 뜻함
- 두 등량곡선은 서로 교차하지 않음
- 등량곡선은 원점에 대해서 볼록한 모양을 가짐
2) 한계기술대체율 체감의 법칙
• 한계기술대체율
- 등량곡선의 기울기의 절대값을 한계기술대체율(Marginal rate of technical substitution, MRTS)이라고 함
• 한 생산요소의 투입을 줄였을 때 같은 생산량을 유지하기 위하여 투입해야 할 다른 생산요소의 양을 의미함
• 한계기술대체율(MRTS)은 두 생산요소의 한계생산의 비율과 같음
• 분모가 세로축에 표시된 생산요소의 한계생산, 이 경우 자본의 한계생산

• 자본의 한계생산

• 노동의 한계생산

• 한계기술대체율 노동의 투입이 증가할수록 체감함
- 자본과 노동의 한계 생산은 체감
- 동일한 등량곡선에서 오른쪽으로 갈수록 노동이 증가하므로 분자는 체감
- 자본이 감소하므로 분모는 체증하므로 한계기술대체율은 체감
Ⅱ. 비용함수
1. 여러 가지 비용의 개념
1) 고정비용과 가변비용
• 고정비용(Fixed cost, FC)
- 산출량에 따라 변하지 않는 비용, 고정생산요소에 지출하는 비용
• 가변비용(Variable cost, VC)
- 산출량에 따라 변하는 비용, 가변생산요소에 지출하는 비용
2) 한계비용과 평균비용
• 한계비용(Marginal cost)
- 산출량을 한 단위 증가시킬 때 총비용의 증가분
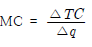
• 평균총비용(Average total cost)
- 산출량 한 단위당 평균비용
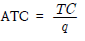
3) 평균가변비용과 평균고정비용
• 평균가변비용(Average variable cost)
- 산출량 한 단위당 평균 가변비용

• 평균고정비용(Average fixed cost)
- 산출량 한 단위당 평균 고정비용

2. 단기: 가변생산요소가 하나인 경우
1) 생산곡선에서 비용곡선으로
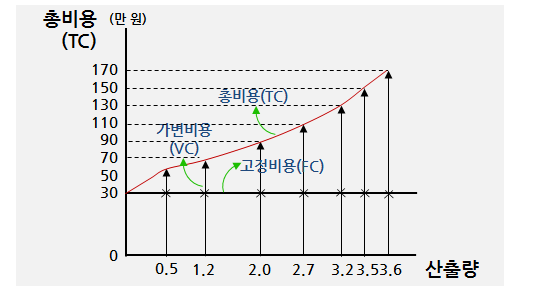
• 앞의 예에서 다음과 같은 표를 얻을 수 있음
- 1번째 열의 생산량을 가로축에 4번째 총비용을 세로축에 그리면 총비용곡선이 됨

- 가래 임대비용이 30만 원, 임금이 20만 원 일 경우
2) 생산함수에서 비용함수로
• 비용은 산출량 수준(q)에 따라 다르고, 생산요소인 자본과 노동의 가격(r, w), 생산기술(H)에 따라 결정
• 총비용함수(Total cost function)은 q, r, w, H의 함수로 표현할 수 있음
• 생산함수 q = g(L)에서 총비용함수 TC = h(q, r, w, H)를 얻을 수 있음
3) 한계생산과 한계비용의 관계
• 단기생산함수가 q = g(L), 임금률을 w라고 하면, 노동의 한계 단위를 고용하는 데 드는 비용은
wΔL임

• 단기에서 노동의 한계생산이 체감한다는 의미와 한계비용이 체증한다는 의미는 표리의 관계임
3. 장기: 가변생산요소가 두 개(자본과 노동)인 경우
1) 등비용곡선(Isocost curve)
• 주어진 총지출의 한도 안에서 구입할 수 있는 노동과 자본의 조합을 의미함
• 등비용곡선의 기울기

• 예시
- r = 30만 원, w = 20만 원이면
: – (20/30) = - (2/3)
2) 비용극소화를 위한 선택
• 산출량(q = 500)을 생산하기 위한 최소비용은 얼마인가?
- 기업이 특정한 생산량을 최소 비용으로 생산하기 위해서는 두 생산요소의 가격을 고려해야 함
- 등량곡선과 등비용곡선이 접하는 점에서 노동과 자본의 선택함으로써 주어진 생산량을 최소비용으로 생산할 수 있는 노동과 자본의 양을 구할 수 있음
- 등량곡선의 기울기 = -MRTS
- 등비용곡선의 기울기

- 비용극소화 조건

- 비용극소화 그래프

: 위의 예에서 산출량 500단위를 생산하기 위한 최적 생산요소의 조합은 F임
: 노동 150단위, 자본 200단위를 투입하는 것이 비용을 최소화하는 방법임
: 총비용 TC = rK + wL = 30 × 100 + 20 × 150 = 600(만 원)
3) 총비용함수
• 총비용함수는 TC = h(q, r, w, H)로 표시할 수 있음
• 기업의 총비용함수
- 상품의 산출량, 자본의 임대가격, 노동의 가격인 임금률, 등량곡선으로 나타낸 생산기술 H에 의해서 결정
: 이 비용극소화 과정에서 경제적인 효율성(Economic efficiency) 개념이 개입됨
4) 전형적인 비용 곡선

• 산출량이 적은 단계에서는 한계생산물이 증가하고 한계비용은 감소함
• 생산량이 계속 증가하면 궁극적으로 한계생산물이 감소하고 한계비용은 증가하므로 평균총비용곡선(ATC)는 U자 모양이 됨
• 한계비용곡선은 평균총비용곡선의 최저점을 통과함
Ⅲ. 단기와 장기의 구분
1. 고정비용과 가변비용의 구분
• 고정비용과 가변비용의 구분은 분속기간에 따라 다름
• 예시
- 자동차 회사는 몇 달 사이에 공장 규모를 조정할 수 없음 따라서 자동차 생산 대수를 늘리려면 더 많은 근로자를 고용할 수밖에 없음
: 공장 비용은 단기적으로는 고정비용이고, 장기적으로는 가변비용임
> 따라서 장기비용곡선과 단기비용곡선은 다름
• 장기 평균총비용곡선은 단기 평균총비용곡선보다 더 완만한 U자형임
• 단기 평균총비용곡선은 장기 평균총비용곡선에 접하거나 그 위에 위치함
- 기업이 단기보다는 장기에 융통성을 발휘할 수 있기 때문임
- 즉, 단기에는 과거의 선택에 기초한 단기 비용곡선 위에서만 생산할 수 있지만, 장기에는 기업이 원하는 단기 비용곡선을 선택할 수 있음

2. 규모의 경제와 규모의 수익
• 규모의 경제(Economies of scale)
- 산출량이 증가함에 따라 평균총비용이 감소하면 규모의 경제가 존재한다고 말함
- 생산기술이 규모의 수익이 증가하는(Increasing Returns to Scale: IRS) 기술
- 생산요소의 가격이 생산량이 변하여도 변하지 않으면 규모의 경제가 발생함
• 규모의 수익이 체증(IRS)
- q = f(K, L)에서 생산요소의 양을 t배로 증가시키면 산출량이 t배 이상 되는 기술
• 규모의 수익이 불변(CRS: Constant Returns to Scale)
- q = f(K, L)에서 생산요소의 양을 t배로 증가시키면 산출량이 t배 되는 기술
• 규모의 수익이 체감(DRS: Deceaasing to Scale)
- q = f(K, L)에서 생산요소의 양을 t배로 증가시키면 산출량이 t배 이하 되는 기술
• 규모의 불경제(diseconomies of scale)
- 산출량이 증가함에 따라 평균총비용이 증가하면 규모의 불경제가 존재한다고 말함
- 생산기술이 규모의 수익이 체감하는(Increasing Returns to Scale: IRS) 기술
- 생산요소의 가격이 생산량이 변하여도 변하지 않으면 규모의 경제가 발생함
'경영학 > 경제학개론' 카테고리의 다른 글
| [경제학개론] 9. 완전경쟁시장 (0) | 2025.04.23 |
|---|---|
| [경제학개론] 8. 시장 공급곡선의 도출 2 (0) | 2025.04.23 |
| [경제학개론] 6. 소비자 이론: 시장 수요곡선의 도출(2) (0) | 2023.06.29 |
| [경제학개론] 5. 소비자 이론: 시장 수요곡선의 도출(1) (0) | 2023.06.28 |
| [경제학개론] 4. 수요와 공급의 탄력성과 시장의 작동원리 (0) | 2023.06.25 |